資訊不對稱
到目前為止,我們已經談了關於賽局理論你所需要知道的一切:所有的玩家戰略和所有的收益。但是我們畢竟活在現實世界,你不可能每次都有辦法了解競爭對手的所有選擇。那麼你要如何知道他們每個選擇的成本和收益?你不可能知道。的確,這樣很難取勝。
大多數時候,當你使用賽局理論時,你必須依賴不完整或是不完全的資訊進行決策。這兩個聽起來好像很像,但是他們有點微妙的差別!
- 不完整的信息意味著有些事情你根本不知道,例如對手的策略或獲益。
- 不完全的信息意味著你不知道對手何時或是否採取行動。
當你坐下來策劃你的賽局時,會發現你的策略不會像我提出的一樣乾淨和完美,到目前為止它很可能看起來像這樣:

填補空白的最好方法是根據你對策略或玩家所知道的策略或收益來推理。這可能比它聽起來容易,像在決策樹中,可能有少量的可能結果。例如,如果你降低你的產品的價格,你的競爭只能以三種方式之一做出反應:降低價格,保持價格或提高價格。同樣,可能很難知道價格變化對您的競爭的具體收益,但您可能理解相對收益(提高價格產生更多收入,同時降低價格降低價格)。
如果你不能填補空白,那麼你可能想考慮不同的賽局。到目前為止,我們已經使用的遊戲的矩陣模型稱為「正常」形式。還有另一種形式的遊戲模型稱為「廣泛」的形式,它也捕獲玩家的決定的順序,可以幫助簡化遊戲缺少信息。如果玩家 1 先行,則上述示例的廣泛形式表示如下:
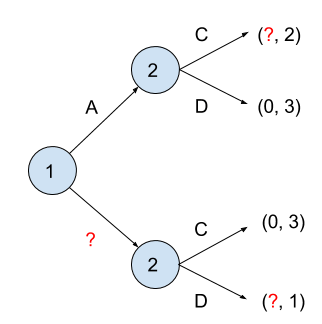
在廣泛的形式建模中,我們從第一個玩家開始移動(在這種情況下為 Player 1)並創建一個圖形,其中邊緣是他們可能的策略(在這種情況下 A 或?,即未知)。每個都導致一個點,其中下一個玩家(玩家 2)在他們的策略之間選擇,這反過來導致收益。這捕獲了遊戲的回合本質,其中一個玩家做出移動,而另一個玩家對它做出反應。
如你所見,這大大簡化了我們不完全的知識問題,因為我們不需要一起擔心所有的未知數!我們只關心下個行動的未知數,以及接下來可能發生的路徑。例如,如果我們是玩家 2 並且玩家 1 選擇策略 A,我們將選擇策略 D,在這個情況下就不需要考慮其他路徑的未知數了 - 因為我們沒有選擇它!
有更先進和正式的方法來計算未知的收益概率,在這個單元沒有辦法窮舉這些方法,但在我的實踐決策的經驗,通過簡單的推理就足以篩除掉大部分不可能發生的結果。
下一章節,我們將談談超過兩個玩家的遊戲!